目录
一、带环问题的解决
1、固定思路
2、思路后的数学证明
3、不相遇的情况分析
二、环入口问题
编辑
1、固定思路
2、数学证明
三、求环的长度
一、带环问题的解决

1、固定思路
链表带环问题比较传统的思路是使用快慢指针,当快和慢指针相遇的时候那么说明此链表带环
所以我们可以很容易写出下面的代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
bool hasCycle(struct ListNode *head)
{ struct ListNode*slow=head;
struct ListNode*fast=head;
while(fast!=NULL&&fast->next!=NULL)
{
fast=fast->next->next;
slow=slow->next;
if(fast==slow)
{
return true;
}
}
return false;
}那么这个是为什么,难道是偶然吗?其实不然。
2、思路后的数学证明

由上面可知道当fast==2slow的时候一定相遇,那么当fast!=2slow呢,一定会相遇吗?,有没有可能出现不相遇的情况?
3、不相遇的情况分析
同样的道理我们还是画图来解释:
理论上来说是存在追不上的情况的,对不对呢?我们通过数学来证明一下: 证明后发现上面的情况可以相遇:
证明后发现上面的情况可以相遇:
那么当fast==任意倍的slow时都是可以的,只不过证明起来比较麻烦,举一个4倍的例子
二、环入口问题
1、固定思路
这个问题也时固定思路设定一个meet指针为fast和slow相遇的地方,newhead为头两个同时向后走当两者相遇时为入口:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode *detectCycle(struct ListNode *head)
{
struct ListNode*slow=head;
struct ListNode*fast=head;
struct ListNode*newhead=head;
struct ListNode*meet=head;
while(1)
{
if(fast==NULL||fast->next==NULL)
{
return NULL;
}
fast=fast->next->next;
slow=slow->next;
if(fast==slow)
{
meet=slow;
break;
}
}
while(newhead!=meet)
{
meet=meet->next;
newhead=newhead->next;
}
return meet;
}2、数学证明
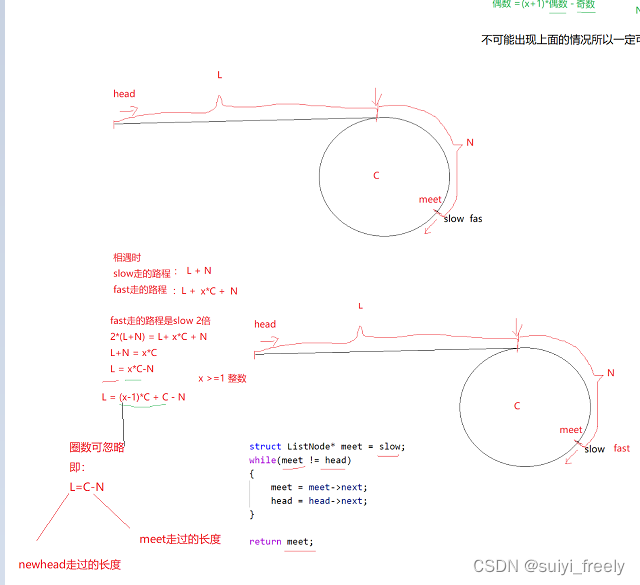
所以上述办法是正确的不是偶然:
三、求环的长度
上述办法求出环的入口,从入口开始走走到再次走到入口时走过的距离就是环长
struct ListNode *cur = meet->next;//避免进不去循环
int count = 0;
while(cur!=meet)
{
cur = cur->next;
count++;
}
count++;//少加了一次